In this blog, we explore the application of identifying the most dominant colours in an image using K-Means Clustering.
Unsupervised Learning in artificial intelligence is a type of machine learning that learns from data without human supervision. Unlike supervised learning, unsupervised machine learning models are given unlabeled data and allowed to discover patterns and insights without any explicit guidance or instruction.
Clustering is an unsupervised machine learning technique. Clustering is the process of building groups of data points in a way that the data in the same group are more similar to one another than to those in other groups.
Clustering algorithms include agglomerative clustering, Gaussian mixtures for clustering, K-Means clustering, hierarchial clustering, DBSCAN, and much more. For the application of extracting dominant colours from an image we make use of the K-Means algorithm (distance-based) over some of the other popular density based clustering algorithms like DBSCAN (popularly used for anomaly detection) Since the similarity between the colours can be simply represented by the location in the 3D space. Many distance-based clustering algorithms, including K-means, are computationally efficient and can handle large datasets, making them suitable for processing images with a large number of pixels. The efficiency of these algorithms allows for faster clustering and analysis of image data.
The K-means algorithms is one of the most popular clustering algorithms. It can cluster groups of data given the number of clusters to form. It begins by selecting n cluster centroids (randomly or using the kmeans++ initialization algorithm) and assigning the data points to each cluster based on its Euclidean Distance from the cluster centroid. A point is considered to be in a particular cluster if it is closer to that cluster’s centroid than any other centroid. K-Means finds the best centroids by alternating between (1) assigning data points to clusters based on the current centroids (2) chosing centroids (points which are the center of a cluster) based on the current assignment of data points to clusters. It continues this process for a number of iterations while trying to minimize the root mean square error each iteration (till the centroids dont change) and improve clustering.
A great example of this can be seen in the figure below taken from this KMeans article.
K-Means Algorithm Visualization Sample
Coming to extracting the most dominant colours in an image, let’s take the example of the following image.
We begin by analyzing the image by extracting the RGB (Red, Green, Blue) values that together make up the colour of the pixel. By making use of the cv2 library from OpenCV, we can essentially “read” the image, i.e. get it’s pixel value, and store the data in a Pandas dataframe for future use. An example of the RGB values for the sample image can be seen below.
Code
import warningswarnings.filterwarnings("ignore")import pandas as pdimport cv2import numpy as npRGB_values = pd.DataFrame(columns=['R', 'G', 'B'])image = cv2.imread("beach.jpg")# get image shapenumPixels = image.shapeprint(numPixels)y, x = numPixels[0], numPixels[1]for i, j inzip(range(y), range(x)): BGR_values = image[i, j] RGB_values.loc[len(RGB_values)] = np.flip(BGR_values) # to get the (B, G, R) values in (R, G, B) formatRGB_values.head(10)
(1200, 1920, 3)
R
G
B
0
161
195
240
1
161
195
240
2
160
194
239
3
159
193
238
4
159
193
238
5
158
192
237
6
157
191
237
7
157
191
237
8
156
190
236
9
156
190
236
A lot of processing libraries, and machine learning algorithms require the data to be scaled or normalized. The colorsys library requires the RGB values to be normalized before being able to convert it into HSL values to generate the plot displaying the colours in the image in a list form! Additionally, since the K-Means clustering algorithm is a distance based algorithm, it is beneficial to rescale each feature dimension of the observation set by its standard deviation so that higher range of some features do not influence the algorithm by acting ‘weighted’. Each feature is normalized across all observations to give it unit variance.
Code
# plot the RGB values on a graphfrom mpl_toolkits import mplot3dimport matplotlibimport matplotlib.pyplot as plt%matplotlib inlineimport colorsys# normalize the RGB valuesRGB_values = RGB_values/255RGB_values.head(5)RGB_unique = RGB_values.drop_duplicates()RGB_unique =list(RGB_unique.to_numpy())RGB_unique.sort(key=lambda rgb: colorsys.rgb_to_hls(*rgb))cmap_RGB = matplotlib.colors.ListedColormap(RGB_unique, "Colours in the image")cmap_RGB
Colours in the image
under
bad
over
We can see below the (R, G, B) values plotted in a 3D space. This visualization is especially important to better analyze the K-Means clustering algorithm.
Code
fig = plt.figure(figsize = (8,8))ax = fig.add_subplot(111, projection='3d')# Data for three-dimensional scattered pointszdata = RGB_values['B']xdata = RGB_values['R']ydata = RGB_values['G']ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='hsv');ax.set_xlabel('R')ax.set_ylabel('G')ax.set_zlabel('B')ax.set_title('RGB value of input image');
Since K-Means clustering requires a defined number of clusters, for accurate clustering, it is important to have an optimum number of clusters, not too less, not too many. We make use of the KElbowVisualizer to find the optimal value for the number of clusters. From the documentation: “The KElbowVisualizer implements the “elbow” method to help data scientists select the optimal number of clusters by fitting the model with a range of values for . If the line chart resembles an arm, then the “elbow” (the point of inflection on the curve) is a good indication that the underlying model fits best at that point. In the visualizer “elbow” will be annotated with a dashed line. The elbow method runs k-means clustering on the dataset for a range of values for k (say from 1-10) and then for each value of k computes an average score for all clusters.” Read More!
We can see from the graph that for our data, 4 is the optimum number of clusters. So our final result would be the 4 most dominant colours in the image.
Below is the algorithm for K-Means clustering with k-means++ initialization from scratch. The K-Means clustering algorithm can also be implemented by using the scikit learn library.
We begin by initializing values such as the dataset in the numpy format, setting the number of clusters, setting the maximum number of iterations, as well as choosing the first centroid at random.
Then, we run the k-means++ algorithm to select the initial centroids. The k-means++ algorithm selects initial cluster centroids using sampling based on an empirical probability distribution of the points’ contribution to the overall inertia. This technique speeds up convergence.
Take one centroid \(c_1\), chosen uniformly at random from the dataset.
Take a new center \(c_i\), choosing an instance \(\mathbf{x}_i\) with probability: \(D(\mathbf{x}_i)^2\) / \(\sum\limits_{j=1}^{m}{D(\mathbf{x}_j)}^2\) where \(D(\mathbf{x}_i)\) is the distance between the instance \(\mathbf{x}_i\) and the closest centroid that was already chosen. This probability distribution ensures that instances that are further away from already chosen centroids are much more likely be selected as centroids.
Repeat the previous step until all \(k\) centroids have been chosen.
After the centroids have been chosen, the K-means algorithm begins running continuously mapping each datapoint to each cluster and improving chosen centroid values until the maximum number of iterations or until there is no change in the centroids chosen.
import mathimport randomx = RGB_values.to_numpy()centroid1 = x[random.randint(0,len(x))]centroids = []centroids.append([centroid1])numClusters = elbow_valueiteration =0max_iter =100# can be passed in as a parameter'''k-means++ '''# pick cluster centroid with probability proportional to the centroid1distance = [math.dist(centroid1, x[i])**2for i inrange(len(x))]for i inrange(1, numClusters):# so above has just chosen the highest dist ones, but we still want random choice where the probability is depending on the distance# also, normalize dists# calculates probabilities prob = distance/np.sum(distance)# choose next centroid with probability proportional to distance squared new_centroid = x[np.random.choice(range(len(x)), size=1, p=prob)] centroids.append(new_centroid)# update distances between newly chosen centroid and other points now distance = [math.dist(new_centroid[0], x[i])**2for i inrange(len(x))]'''K-means algorithm'''centroids = np.array(centroids)prev_centroids = np.zeros(centroids.shape)while np.not_equal(centroids, prev_centroids).any() and iteration < max_iter:# Sort each datapoint, assigning to nearest centroid# sorted points is of size num_clusters, num_points in each cluster sorted_points = [[] for _ inrange(numClusters)]for point in x: dists = [math.dist(point, np.squeeze(i)) for i in centroids] centroid_idx = np.argmin(dists) sorted_points[centroid_idx].append(point)# Push current centroids to previous, reassign centroids as mean of the points belonging to them# new centroid is mean of the points in each cluster prev_centroids = centroids[:] centroids = [np.mean(cluster, axis=0) for cluster in sorted_points]# make sure that none of the centroid values are nanfor points inrange(len(centroids)):if np.isnan(centroids[points]).any(): centroids[points] = prev_centroids[points] iteration +=1
Plotting the clusters formed after K-Means clustering algorithm as shown below.
Code
colors = []for i in centroids: r, g, b = i colors.append(( r, g, b ))fig = plt.figure(figsize = (8,8))ax = fig.add_subplot(111, projection='3d')# plot the sorted clustersfor i inrange(len(sorted_points)): a, b, c =zip(*sorted_points[i]) ax.scatter(a, b, c, s =40 , color = colors[i], marker ='o', label ="cluster "+str(i)) label ="centroid of cluster"if i ==len(sorted_points)-1else"" ax.scatter(colors[i][0], colors[i][1], colors[i][2], s =100 , marker ='x', color = [0,0,0], label = label)ax.set_xlabel('R')ax.set_ylabel('G')ax.set_zlabel('B')ax.legend()plt.show()
We can visualize the following to be the most dominant colours in the given image!
Code
plt.grid(False)plt.imshow([colors])plt.show()
Code
total_points =len(RGB_values.to_numpy())labels = ['Colour'+str(i+1) for i inrange(len(colors))]sizes = [len(sorted_points[i])/total_points for i inrange(len(sorted_points))]fig, ax = plt.subplots()ax.pie(sizes, colors=colors, autopct='%1.1f%%', pctdistance=1.15);
And we’re done!
Source Code
---title: "Clustering with K-Means"author: "Anushka S"date: "2023-12-03"categories: [Clustering, Unsupervised Learning, Machine Learning, K-Means]---In this blog, we explore the application of identifying the most dominant colours in an image using K-Means Clustering. [Unsupervised Learning](https://cloud.google.com/discover/what-is-unsupervised-learning#:~:text=Unsupervised%20learning%20in%20artificial%20intelligence,any%20explicit%20guidance%20or%20instruction.) in artificial intelligence is a type of machine learning that learns from data without human supervision. Unlike supervised learning, unsupervised machine learning models are given unlabeled data and allowed to discover patterns and insights without any explicit guidance or instruction. Clustering is an unsupervised machine learning technique. Clustering is the process of building groups of data points in a way that the data in the same group are more similar to one another than to those in other groups.Clustering algorithms include agglomerative clustering, Gaussian mixtures for clustering, K-Means clustering, hierarchial clustering, DBSCAN, and much more. For the application of extracting dominant colours from an image we make use of the K-Means algorithm (distance-based) over some of the other popular density based clustering algorithms like DBSCAN (popularly used for anomaly detection) Since the similarity between the colours can be simply represented by the location in the 3D space. Many distance-based clustering algorithms, including K-means, are computationally efficient and can handle large datasets, making them suitable for processing images with a large number of pixels. The efficiency of these algorithms allows for faster clustering and analysis of image data. The K-means algorithms is one of the most popular clustering algorithms. It can cluster groups of data given the number of clusters to form. It begins by selecting n cluster centroids (randomly or using the kmeans++ initialization algorithm) and assigning the data points to each cluster based on its Euclidean Distance from the cluster centroid. A point is considered to be in a particular cluster if it is closer to that cluster's centroid than any other centroid. K-Means finds the best centroids by alternating between (1) assigning data points to clusters based on the current centroids (2) chosing centroids (points which are the center of a cluster) based on the current assignment of data points to clusters. It continues this process for a number of iterations while trying to minimize the root mean square error each iteration (till the centroids dont change) and improve clustering. A great example of this can be seen in the figure below taken from this [KMeans article](https://stanford.edu/~cpiech/cs221/handouts/kmeans.html).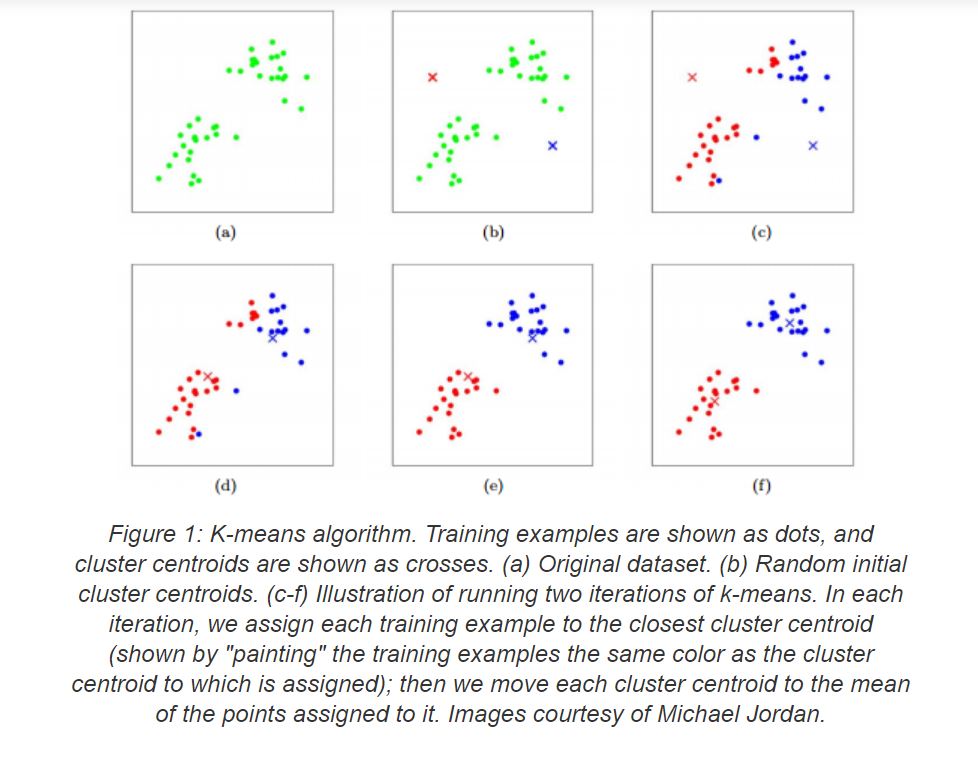{width=80%}Coming to extracting the most dominant colours in an image, let's take the example of the following image.{width=80%}We begin by analyzing the image by extracting the RGB (Red, Green, Blue) values that together make up the colour of the pixel. By making use of the [cv2](https://opencv.org/) library from OpenCV, we can essentially "read" the image, i.e. get it's pixel value, and store the data in a [Pandas](https://pandas.pydata.org/docs/index.html#) dataframe for future use. An example of the RGB values for the sample image can be seen below.```{python}import warningswarnings.filterwarnings("ignore")import pandas as pdimport cv2import numpy as npRGB_values = pd.DataFrame(columns=['R', 'G', 'B'])image = cv2.imread("beach.jpg")# get image shapenumPixels = image.shapeprint(numPixels)y, x = numPixels[0], numPixels[1]for i, j inzip(range(y), range(x)): BGR_values = image[i, j] RGB_values.loc[len(RGB_values)] = np.flip(BGR_values) # to get the (B, G, R) values in (R, G, B) formatRGB_values.head(10)```A lot of processing libraries, and machine learning algorithms require the data to be scaled or normalized. The colorsys library requires the RGB values to be normalized before being able to convert it into HSL values to generate the plot displaying the colours in the image in a list form! Additionally, since the K-Means clustering algorithm is a distance based algorithm, it is beneficial to rescale each feature dimension of the observation set by its standard deviation so that higher range of some features do not influence the algorithm by acting 'weighted'. Each feature is normalized across all observations to give it unit variance.```{python}# plot the RGB values on a graphfrom mpl_toolkits import mplot3dimport matplotlibimport matplotlib.pyplot as plt%matplotlib inlineimport colorsys# normalize the RGB valuesRGB_values = RGB_values/255RGB_values.head(5)RGB_unique = RGB_values.drop_duplicates()RGB_unique =list(RGB_unique.to_numpy())RGB_unique.sort(key=lambda rgb: colorsys.rgb_to_hls(*rgb))cmap_RGB = matplotlib.colors.ListedColormap(RGB_unique, "Colours in the image")cmap_RGB```We can see below the (R, G, B) values plotted in a 3D space. This visualization is especially important to better analyze the K-Means clustering algorithm.```{python}fig = plt.figure(figsize = (8,8))ax = fig.add_subplot(111, projection='3d')# Data for three-dimensional scattered pointszdata = RGB_values['B']xdata = RGB_values['R']ydata = RGB_values['G']ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='hsv');ax.set_xlabel('R')ax.set_ylabel('G')ax.set_zlabel('B')ax.set_title('RGB value of input image');```Since K-Means clustering requires a defined number of clusters, for accurate clustering, it is important to have an optimum number of clusters, not too less, not too many. We make use of the KElbowVisualizer to find the optimal value for the number of clusters. From the documentation: "The KElbowVisualizer implements the “elbow” method to help data scientists select the optimal number of clusters by fitting the model with a range of values for . If the line chart resembles an arm, then the “elbow” (the point of inflection on the curve) is a good indication that the underlying model fits best at that point. In the visualizer “elbow” will be annotated with a dashed line. The elbow method runs k-means clustering on the dataset for a range of values for k (say from 1-10) and then for each value of k computes an average score for all clusters." [Read More!](https://www.scikit-yb.org/en/latest/api/cluster/elbow.html)We can see from the graph that for our data, 4 is the optimum number of clusters. So our final result would be the 4 most dominant colours in the image.```{python}#| code-fold: falseimport sklearn.clusterfrom yellowbrick.cluster import KElbowVisualizermodel = KElbowVisualizer(sklearn.cluster.KMeans(), k=10)model.fit(RGB_values.to_numpy());model.show();elbow_value = model.elbow_value_```Below is the algorithm for K-Means clustering with k-means++ initialization from scratch. The K-Means clustering algorithm can also be implemented by using the [scikit learn library](https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html).We begin by initializing values such as the dataset in the [numpy](https://numpy.org/doc/stable/index.html) format, setting the number of clusters, setting the maximum number of iterations, as well as choosing the first centroid at random.Then, we run the k-means++ algorithm to select the initial centroids. The k-means++ algorithm selects initial cluster centroids using sampling based on an empirical probability distribution of the points' contribution to the overall inertia. This technique speeds up convergence.* Take one centroid $c_1$, chosen uniformly at random from the dataset.* Take a new center $c_i$, choosing an instance $\mathbf{x}_i$ with probability: $D(\mathbf{x}_i)^2$ / $\sum\limits_{j=1}^{m}{D(\mathbf{x}_j)}^2$ where $D(\mathbf{x}_i)$ is the distance between the instance $\mathbf{x}_i$ and the closest centroid that was already chosen. This probability distribution ensures that instances that are further away from already chosen centroids are much more likely be selected as centroids.* Repeat the previous step until all $k$ centroids have been chosen.After the centroids have been chosen, the K-means algorithm begins running continuously mapping each datapoint to each cluster and improving chosen centroid values until the maximum number of iterations or until there is no change in the centroids chosen.```{python}#| code-fold: false#| code-line-numbers: trueimport mathimport randomx = RGB_values.to_numpy()centroid1 = x[random.randint(0,len(x))]centroids = []centroids.append([centroid1])numClusters = elbow_valueiteration =0max_iter =100# can be passed in as a parameter'''k-means++ '''# pick cluster centroid with probability proportional to the centroid1distance = [math.dist(centroid1, x[i])**2for i inrange(len(x))]for i inrange(1, numClusters):# so above has just chosen the highest dist ones, but we still want random choice where the probability is depending on the distance# also, normalize dists# calculates probabilities prob = distance/np.sum(distance)# choose next centroid with probability proportional to distance squared new_centroid = x[np.random.choice(range(len(x)), size=1, p=prob)] centroids.append(new_centroid)# update distances between newly chosen centroid and other points now distance = [math.dist(new_centroid[0], x[i])**2for i inrange(len(x))]'''K-means algorithm'''centroids = np.array(centroids)prev_centroids = np.zeros(centroids.shape)while np.not_equal(centroids, prev_centroids).any() and iteration < max_iter:# Sort each datapoint, assigning to nearest centroid# sorted points is of size num_clusters, num_points in each cluster sorted_points = [[] for _ inrange(numClusters)]for point in x: dists = [math.dist(point, np.squeeze(i)) for i in centroids] centroid_idx = np.argmin(dists) sorted_points[centroid_idx].append(point)# Push current centroids to previous, reassign centroids as mean of the points belonging to them# new centroid is mean of the points in each cluster prev_centroids = centroids[:] centroids = [np.mean(cluster, axis=0) for cluster in sorted_points]# make sure that none of the centroid values are nanfor points inrange(len(centroids)):if np.isnan(centroids[points]).any(): centroids[points] = prev_centroids[points] iteration +=1```Plotting the clusters formed after K-Means clustering algorithm as shown below.```{python}colors = []for i in centroids: r, g, b = i colors.append(( r, g, b ))fig = plt.figure(figsize = (8,8))ax = fig.add_subplot(111, projection='3d')# plot the sorted clustersfor i inrange(len(sorted_points)): a, b, c =zip(*sorted_points[i]) ax.scatter(a, b, c, s =40 , color = colors[i], marker ='o', label ="cluster "+str(i)) label ="centroid of cluster"if i ==len(sorted_points)-1else"" ax.scatter(colors[i][0], colors[i][1], colors[i][2], s =100 , marker ='x', color = [0,0,0], label = label)ax.set_xlabel('R')ax.set_ylabel('G')ax.set_zlabel('B')ax.legend()plt.show()```We can visualize the following to be the most dominant colours in the given image!```{python}plt.grid(False)plt.imshow([colors])plt.show()``````{python}total_points =len(RGB_values.to_numpy())labels = ['Colour'+str(i+1) for i inrange(len(colors))]sizes = [len(sorted_points[i])/total_points for i inrange(len(sorted_points))]fig, ax = plt.subplots()ax.pie(sizes, colors=colors, autopct='%1.1f%%', pctdistance=1.15);```And we're done!